應用二階段微分演化演算法(第54期)
摘要
國內空調系統耗電量約占住商建築物耗電量的 45% 以上 ,其中冰水主機就占空調系統耗電 量的 70% 以上 。半導體產業無塵室的空調系統耗電 量更為一般建築物的 5-10 倍 。因此冰水主機最小耗 能運轉是建築物節能的重要課題 。本研究提出二階 段微分演化演算法求解冰水主機負載最佳化 (optimal chiller loading,簡稱OCL)問題。二階段微分演化 演算法整合二進制微分演化演算法的全域廣度搜尋 (exploration)與實數微分演化演算法區域深度搜尋 (exploitation) 的優點 ,藉由找尋冰水主機群最小能耗 操作點 ( 操作策略 ),達到空調系統節能目的 。本研 究方法與其他參考文獻比較 ,其結果二階段微分演 化演算法可達到等於或優於其他演算法 。因此證明 二階段微分演化演算法可適用於冰水機群負載最佳化問題 。
一、 前言
根據統計 ,國內大用戶建築之空調設備用電約佔 32%~54%,而冰水主機佔整體空調耗電的 70% 以上 ,佔能源負擔極高的比重 [1]。多台冰水主機並 聯運轉的系統 ( 多冰水主機系統 ) 中 ,每台冰水主機 可獨立運轉 ,所以可藉由冰水主機彼此間的運轉排 程調度方式來提供場域穩定冷凍頓備載量與高彈性的 檢修調度 [1],在大型的商辦建物內是很常見的 。由於多冰水主機系統是由不同特性甚至是不同類型 的冰水主機所組成 ,如何能夠調配適當的冰水主 機組運轉台數與運轉控制點 ,使每部主機在最佳 效率下運轉為空調水系統一重要的節能關鍵 。
近年來已有許多文獻探討多冰機系統的最佳負 載分配(optimal chiller loading,簡稱OCL)問題。 Chang[2,3] 提出分支界定法與拉格蘭傑乘數法應 用於求解多冰水主機負載最佳化問題 。除傳統數 值方法外 ,許多啟發式的最佳化方法也大量運 用在求解 OCL 問題上 。藉由物種演化理論之的 基因演化法(Genetic Algorithm,簡稱GA)[4]可以 找到較文獻 [2,3] 耗電更低的多冰水主機負載組 合。Chang等人[5]將進化策略演算法(Evolution Strategy,簡稱ES)應用於OCL問題,可找出更 低且更高精度的冰機組耗電 。利用群體間的社會 行為作為演化基礎的粒子群演算法(Particle swarm optimization,簡 稱 PSO) 應 用 在 OCL 問 題 上 [6], PSO 在 OCL 的求解上較二進制 GA 與實數 GA 來 得更有效率 。以群體間差異性來進行演化的微 分演化演算法(Differential Evolution,簡稱DE) 亦被應用於 OCL 問題上 [7],依據文獻所述其結 果較粒子群演化法來得更好 。Coelho 等人 [8] 提 出將差分杜鵑鳥演化法(differential cuckoo search approach)來改良原有的杜鵑鳥搜尋法(cuckoo search approach),使其應用於OCL問題上的效能 相較於 GA、PSO 與 DE 來得更好 。
全域搜尋廣度的探勘(exploration)與區域搜尋 深度的開發 (exploitation) 為影響演化式最佳化方 法二個重要因素 ,二者的平衡 ,直接影響到最 佳解的搜尋的結果與效能 。Tan[9] 等人動態調整 演化式運算以維持多目標最佳化的廣度與收斂 的平衡 。Binkley[10] 等人運用粒子群演算法進行 多值域最佳化 ,當粒子群速度低於閥值 ,亦即 改變設計量變小 ,將粒子重新起始化 ,以保持 多值域搜尋廣度 。Epitropakis[11] 等人組合不同 的微分演化演算法的突變機制 ,先使用利於廣 度搜尋的機制 ,再用收斂性高的機制搜尋最佳 解 。Bao[12] 提出混合蟻群演算法及模擬退火法 二階段最佳化演算法 ,解決複雜的最佳化問題 。
Beghi[13] 等人運用多階段基因演算法多冰水主機 的有效管理 ,以降低耗電量及運作成本 。Cheng 及 Tran[14] 運用二階段微分演化驗算法專案計畫 時間與成本的最佳化 。
本文提出二階段微分演化演算法求解冰水主機 負載最佳化問題 ,其架構包含兩種不同變數類型 的微分演化法 : 第一階段運用改良式二進制微分 演化演算法(Modified Binary Differential Evolution 簡稱 MBDE)[15,16] 進行全域的廣度搜尋 ,第二 階段使用實數微分演化演算法進行區域的深度搜 尋 。二進制編碼方式較實數編碼的演算法有更高 的全域搜尋廣度 [17],故在搜尋最佳解的過程中 可以快速地找出全域最佳解的所在區域 。在第一 階段 MBDE 完成後 ,將其最佳解經過實數轉換 後代入第二階段的實數 DE 中進行更深度的區域 最佳化搜尋 。透過上述兩階段的整合 ,二階段 微分演化演算法整合二進位 MBDE 與實數 DE 的 優點 ,使其具備良好的全域廣度與區域深度的搜 尋能力 ,提高整體演化法搜尋最佳解的執行效能 與結果 。
本文的架構如下 : 第二節為描述冰水主機負載 最佳化問題細節與其目標函式和限制條件 。第三 節為二階段微分演化演算法之演化機制與特性說 明 。第四節為範例結果比較 。第五則是結論 。
二、 多冰機系統介紹
多冰水主機系統可提供彈性運轉 、備載容量及 較少的系統停機維修 ,被廣泛的應用在許多大型 建物的空調系統中 。多冰水主機系統是由兩台以 上的冰水主機並聯而成 ,多冰水主機系統中的每 一台冰水主機皆可獨立運作並供應不同的冷凍能 力 ,依不同或相同的性能曲線高效率運轉 ,來 提供場域多樣化的空調冷凍噸需求 ,其架構如下 圖 1 所示 。
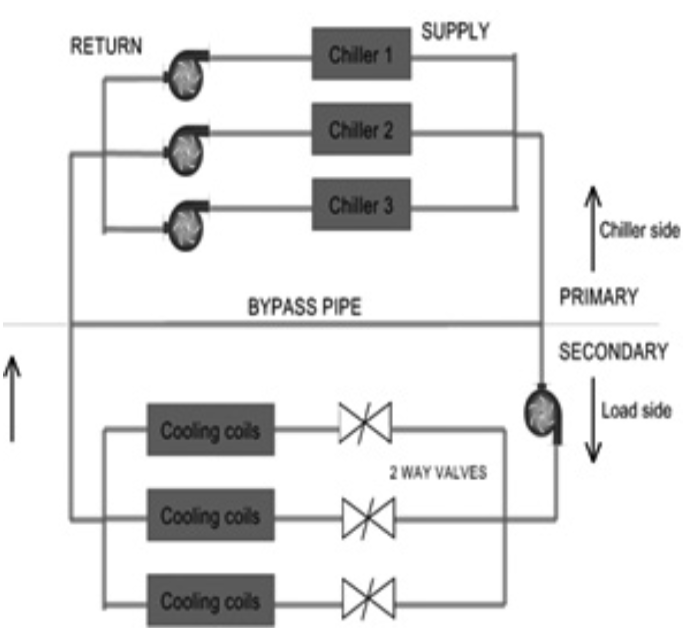
一般冰水主機會以滿足最大尖峰負載需求作為 最大容量設計考量 ,但因實際場域需求與季節變 換的關係 ,最大尖峰負載的時間通常僅是發生在 夏季的尖峰用電時間 ,而其他大部份運轉在部 份負荷條件下 ,所以造成設計量過大且耗費能 源,冰水主機的部份負載率(partial load rate,簡 稱 PLR) 關係式可表示為 (1) 式 :

冰水主機耗電量與 PLR 有相當程度的關聯 ,依 參考文獻 [8] 所建立的冰水主機耗電方程式如 (2) 式及(3)式所示:
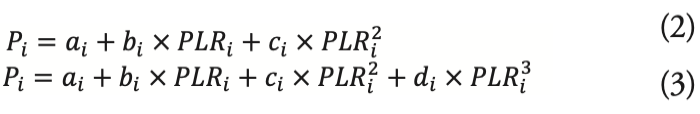
上式 (2) 為範例 1 之冰水主機耗電模型計算式 , (3) 式則是範例 2 的冰水主機耗電模型 。公式中 的係數 ai、bi、ci 與 di 則是依照文獻 [8] 來定義分 析範例中每一台冰機的耗電與部分負載率的關
係 。部分負載率的上下限範圍從 0.0~1.0。
整體 OCL 最佳化的目的是依場域冷凍負載需 求找出多冰水機系統每台冰水主機的部分負載 , 達到整體最低耗電量的目標 。故在本文 OCL 最佳化的目標函式定義如式 (4):
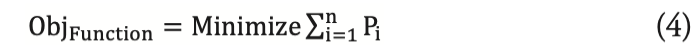
上述式(4)中,參數i是指第i台的冰機代號,n 為整個多冰機系統的冰機總數 ,Pi 是指第 i 台冰 機的耗電值 ( 單位 kW)。目標方程式即找出多冰機系統中的總耗電最低 。
OCL 問題在求解時包含兩種限制條件 [8],第一個限制條件是總和輸出的冷凍噸數值必須等於 場域之冷凍噸數需求 ,如下 (5) 式是所示 。Qi 是 指第 i 台冰機的額定冷凍噸容量 ,CL 是場域所需 之總冷凍噸 。

第二個限制條件則是每一台冰機的部分負載率不能低於 30%[8],其定義如下 (6):

三、 二階段微分演化演算法
二階段微分演化演算法為一整合改良式二進制 微分演化法 (MBDE) 與微分演化法 (DE) 之最佳化 方法 ,可在搜尋最佳解時具備較好的廣度搜尋與 收斂速度 。
1. 微分演化演算法
微分演化演算法是由Price和Storn於1995 年提出 [18],首先隨機產生設計範圍的初始實數個 體 ,經由突變機制亂數選取不同個體產生向量差 作為搜尋方向 ,再乘上一個權重作為搜尋步伐大 小 ,形成新的搜尋向量 ,再經由交配 、評估與 選擇 ,重複迭代直到滿足終止條件為止 。微分 演化演算法的主要三個步驟為:突變 、交配和選擇。
1.1 突變機制(Mutation operator)
微分演算法的突變機制其目的是為了產生與母代不同的向量 ,稱為干擾向量 ,干擾向量由方 程式產生 ,如方程式 (7)、(8) 所示 ,G 代表目前 代數。

由族群的個體1 到P中亂數選取兩個r1 和r2 不 同個體 ,將目標向量 Xr1,G 和 Xr1,G 相減形成一 向量差 ,再乘上權重值 F,最後再加上當代最好 的目標向量 Xbest,G 或本體向量 Xi,G 來得到下一 代干擾向量 。
1.2 交配機制(Crossover operator)
個體經由突變產生的干擾向量後由交配機制進行產生嘗試向量 ,交配機制的機率 Cr 範圍介於 0.0~1.0,與亂數產生的 R 值來比較 ,若 R 值大於 Cr 值則選擇初始向量 ( 沒突變的向量個體 ),若 R 值小於 Cr 值則選擇干擾向量做為下一代的嘗試 向量 。其交配機制的方程式如 (9) 所示 :

2. 改良式二進制微分演算法(MBDE)
改良式微分演算法[15,16]由Wu和Tseng於2010 年提出 ,將原本微分演算法實數編碼改良成二進制編碼並使用改良的突變機制進行演化 , 該方法亦有應用於工程最佳化問題上 [19]。其改良式二進制微分演算法的機制與原微分演化法相同。
2.1 突變機制
改良式微分演算法的突變方程式為 (10)、(11)二式 ,由原微分演化演算法突變機制改進而來 [18],此機制使用邏輯機制運算二進位字串 。此 二進制突變藉由 XOR 邏輯機制把字串分成兩組 , 經由 XOR 邏輯機制分成一組為“ 0”、一組為“ 1” 的字串 ,為“ 0”的那組字串為兩個體共同特徵 , 再用設定的權重值 F2 與亂數產生的值去比較 , 當亂數產生的值小於權重值 F2,則將字元“ 0” 或“ 1”突變為“ 1”或“ 0”,反之當亂數產生的 值大於權重值 F2,則將字元保持不變 ,而“ 1” 的那組字串表示兩個體不同特徵 ,再用設定的 權重值 F1 與亂數產生的值去比較 ,當亂數產生 的值小於權重值 F1,則將字元“ 0”或“ 1”突變 為“ 1”或“ 0”。反之當亂數產生的值大於權重值 F1,則將字元保持不變 ,最後合併兩組字串成為下一代干擾向量 Vi,G+1,如改良的二進制突變 方程式流程圖如 2 所示 。
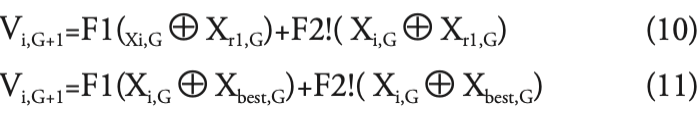
權重值 F1 會大於權重值 F2,因為有較高機率 最佳解的特徵為共同特徵 ,故以較低機率保持共 同特徵 ,較高機率變動不同特徵 。

圖2... 改良的二進制突變機制[15]
2.2 交配機制
改良二進制微分演化演算法二進制交配機制如同微分演算法交配機制 ,由互相對等的第 j 個設 計變數經由亂數產生的值與設定的交配率做比 較 ,若亂數產生的值大於交配率 ,則選目標向 量做為下一代的嘗試向量 ,反之若亂數產生的值 小於交配率 ,則選干擾向量做為下一代的嘗試向 量,如圖3 所示。

圖3... 二進制交配機制[15]
2.3 選擇機制
如同微分演算法的評估與選擇 ,經由二進制突變和二進制交配 ,再比較初始向量的目標函數值 F(Xi,,G) 和嘗試向量的目標函數值 F(Ui,G+1),取 最好的成為下一代的目標向量 Xi,G+1。整體演化 方式重複步驟 2.1、2.2 與 2.3 進行疊代直到滿足 終止條件為止 。
3. 二階段微分演化演算法
二階段微分演化演算法是將 OCL 的問題分成兩個階段進行求解 ,在第一階段的 MBDE 求解 時,將每台冰水主機的PLR進行二進制編碼, 並帶入限制條件與目標方程式定義後開始求解 。 由於二進制編碼的數值解析度較低但具備較高的 搜尋廣度 [17],故當第一階段求解完成後會將結 果 ( 亦即可行解 ) 解碼成實數型態 ,帶入第二階 段 DE 進行深度的求解 。整體二階段微分演化演 算法架構如下圖 4 所示 :

圖4... 二階段微分演化法架構圖
四、 結果分析與討論
本研究選擇參考文獻 [8] 中 OCL 問題做為二階 段微分演化演算法的測試範例 。測試範例為求解 六台冰水機系統的 OCL 問題 。本研究的設定參 數如下 : 個體數為 20 個 、微分演化法的突變率與 交配率設定為 0.5、改良二進制微分演化演算法 的交配率設定為 0.5,其突變率 F1 與 F2 分別設定 為0.5 與0.005、上述參數設定均參考文獻[15]、 [18] 建議值來進行 。演化代數是符合分析範例之 計算次數需求行來設定 ,測試範例的演化代數設 定為 1,000 代 。
1. 測試範例
測試範例為六台冰水主機所組成之多冰水主機系統 ,目的為計算出該六台冰水主機在不同冷凍 噸需求時的最低耗電組合 ,分析範例一場域冷 凍噸需求分別為6858 (90%)、6477 (85%)、6096 (80%)、5717 (75%)與5334 (70%)等五種。分析 範例一之冰水主機的耗電為公式 (2),每台冰水 機可提供之額定冷凍噸與耗電參數 (ai、bi、ci), 如表 1 所示 。本研究採用與其他文獻 [8] 相同的比較方式 ,計算次數為 20,000 次 ,並連續執行 30 次以計算出平均值 ,標準差 ,最大極值與最 小極值 。
表1... 測試範例-耗電係數與額定冷凍噸資訊
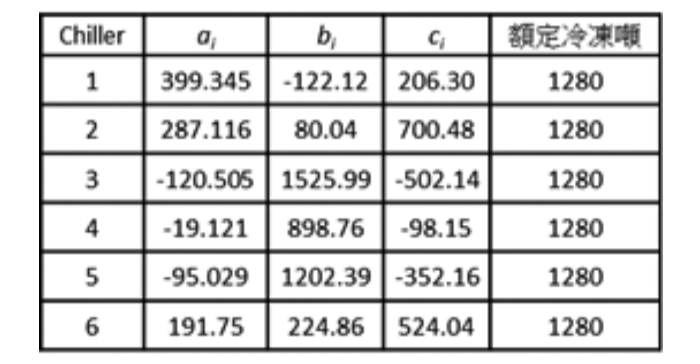
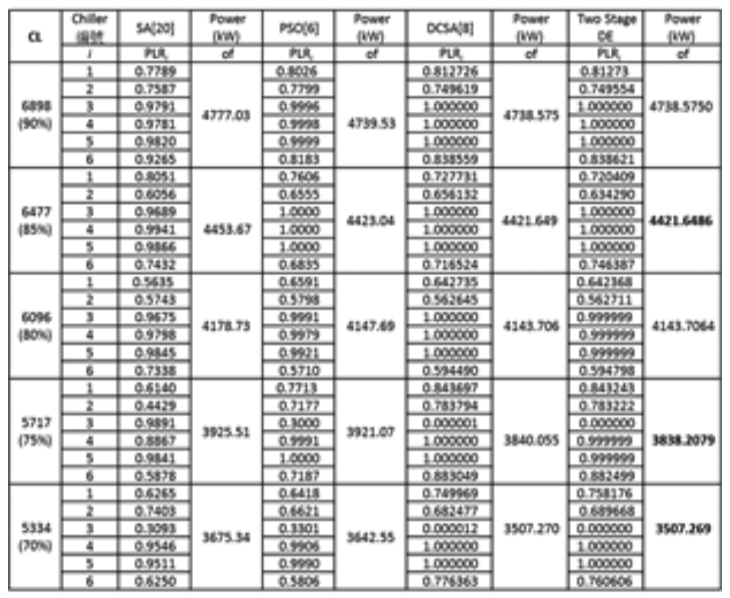
表2 為DCSA[8]與本文方法的最佳化結果比 較 ,可以發現二階段微分演化演算法在不同 CL 條件下所找到的最佳化答案不論是最小極值或是 標準差值均能與文獻相似,甚至在CL為80%、 75% 與 70% 的條件下能達到 DCSA 更好的結果 。 表 3 為二階段微分演化演算法與其他方法的最佳 解比較,在CL為90%與80%可以得到與DCSA 相似的解且優於 SA[20] 與 PSO[6]。在其他 CL 條 件下 (85%、75% 與 70%) 則二階段微分演化法的結果均優於其他文獻 [6][8][20]。
表2 分析範例1-與DCSA比較

表3... 分析範例1-與其他文獻方法比較
五、 結論
提出之二階段微分演化演算法整合二進制與實 數微分演化演算法的不同特性 ,同時具備良好的 最佳解搜尋廣度與收斂速度 。由測試範例的結果 與其他文獻的結果比較可以明顯證明本文所提出 二階段微分演化演算法適用於多冰水主機系統的 最低耗電組合最佳化 。不但可以得到與參考文獻 相近甚至更好的最佳解外 ,每次搜尋到最佳解的 差異度均比文獻來得更好 。更加確認二階段微分 演化演算法的效能與穩定性比目前其他方法來的 更好 ,可適用於相同類型的最佳化問題 。
補充說明
原文曾刊登在冷凍空調&能源科技期刊 105 期 ,本文為原作者精簡後版本 。
